이 글은 Graphical Model에 대해서 정리한 내용입니다.
Graphical Models
Graphical Model이란 확률 변수(Random Variables)들의 조건부 식을 시각적으로 표현한 모델이며 복잡한 확률 분포를 표현하고 분석하는데 사용됩니다. 또한 확률 변수들 간의 관계를 이해할 수 있는 것이 장점입니다.
베이지안 네트워크
베이지안 네트워크는 방향성 비순환 그래프(DAG)를 사용하여 확률변수 간의 관계를 표현합니다.
방향성 비순환 그래프 : 모든 Edges가 방향을 가지며 한쪽 방향으로만 이동할 수 있습니다. 그리고 그래프 내에 순환(Cycle)이 존재하지 않습니다. 즉, 어느 노드에서 출발하여 방향을 따라 이동하다 다시 원래 노드로 돌아오는 경로가 없습니다.
노드(Node)는 확률 변수를 나타내고, 엣지(Edges)는 변수들 간의 관계를 나타냅니다.

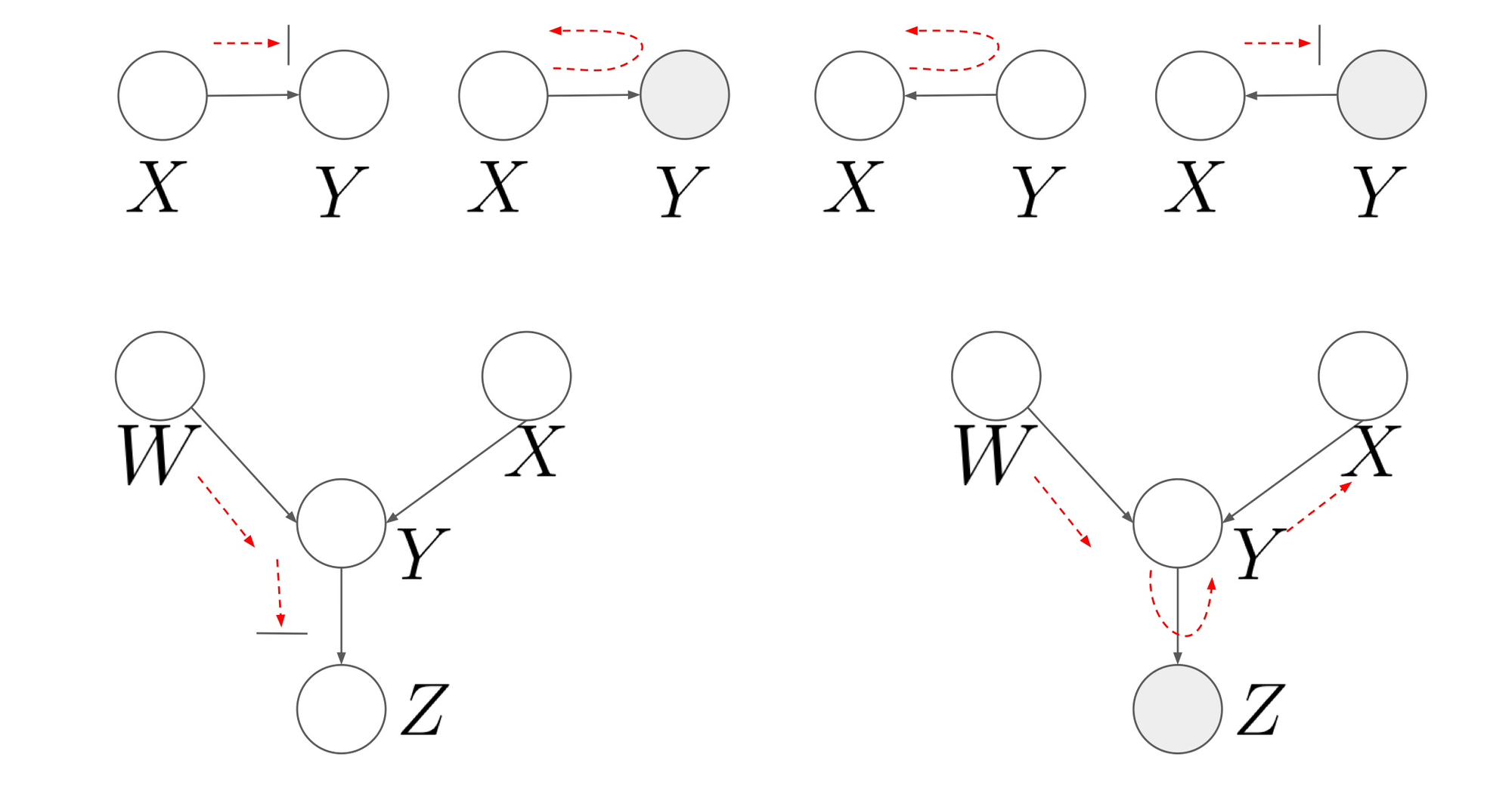
위 그림은 X와 Y의 확률변수가 있을 때 Y변수는 X로부터 정보를 받는다고 볼 수 있습니다. X에 의해 Y의 확률분포가 달라진다고 볼 수 있으며 $P(Y|X)$형태의 조건부 확률로 나타낼 수 있습니다.
The Bayes ball algorithm
다음은 Bayes ball algorithm에 대해 다뤄볼 건데, 그 전에 독립과 조건부 독립의 정의를 보고 가겠습니다.
Definition of independence
X와 Y가 독립인 경우 $X\perp Y$ 로 표현이 되며 아래와 같이 사용할 수 있습니다.
$P(X,Y)=P(X)P(Y)$
$P(X|Y)=\frac{P(X,Y)}{P(Y)}=\frac{P(X)P(Y)}{P(Y)}=P(X)$
$P(Y|X)=P(Y)$
Definition of conditional independence
Z가 주어(Given)졌을 때 X와 Y가 독립인 경우 $X\perp Y|Z$ 로 표현이 되며 아래와 같이 사용할 수 있습니다.
$P(X,Y|Z)=P(X|Z)P(Y|Z)$
$P(X|Y,Z)=P(X,Y|Z)*\frac{P(Z)}{P(Y,Z)}=P(X|Z)P(Y|Z)\frac{1}{P(Y|Z)}=P(X|Z)$
$P(Y|X,Z)=P(X,Y|Z)*\frac{P(Z)}{P(X,Z)}=P(X|Z)P(Y|Z)\frac{1}{P(X|Z)}=P(Y|Z)$
Bayes ball algorithm에 필요한 개념을 다뤄보았고 이제는 Bayes ball algorithm에서 3가지 유형에 대해 다뤄보겠습니다. (Chain Structure, Fork structure, inverse Fork structure)
Chain Structure(head-to-tail)

위 그림은 Chain Structure라고 부르며 joint probability distribution은 다음과 같습니다.
$p(x,y,z)=p(x)p(y|x)p(z|y)$
원래의 joint pdf는 $p(x,y,z)=p(x)p(y|x)p(z|x,y)$이지만, 위 그림에서는 사실 Y는 X에 대한 정보를 받고 있기 때문에 $p(z|y)=p(z|x,y)$가 됩니다.
Q : X와 Z가 독립인가?
A : NO!
Why?
$p(x,z)=p(z|x)p(x)=p(z|x,y)p(x)=p(z|y)p(x)\neq p(z)p(x)$
(아까 위에서 Definition of independence에서 3가지 중 한개라도 성립하거나 성립하지 않는다는 것을 보여 증명할 수 있습니다.)

Q : Y가 주어졌을 때 X와 Z가 조건부 독립인가?
A : Yes!
Why?
$p(x|y,z)=\frac{p(x,y,z)}{p(y,z)}=\frac{p(x)p(y|x)p(z|y)}{p(z|y)p(y)}=\frac{p(x,y)}{p(y)}=p(x|y)$
(마찬가지로 위에서 Definition of conditional independence에서 3가지 중 한개라도 성립하거나 성립하지 않는다는 것을 보여 증명할 수 있습니다.)
Fork Structure(tail-to-tail)

$p(x,y,z)=p(y)p(x|y)p(z|y)$
Q : X와 Z가 독립인가?
A : NO!
Why?
$p(x,z)=\Sigma_yp(x,z,y)=\Sigma_yp(y)p(x|y)p(z|y)$
$p(x)=\Sigma_yp(x,y)=\Sigma_yp(y)p(x|y)$
$p(z)=\Sigma_yp(z,y)=\Sigma_yp(y)p(z|y)$
$p(x,z)\neq p(x)p(z)$

Q : Y가 주어졌을 때 X와 Z가 조건부 독립인가?
A : Yes!
Why? $p(x,y,z)=p(y)p(x|y)p(z|y)$
$\frac{p(x,y,z)}{p(y)}=p(x|y)p(z|y) \rightarrow p(x,z|y)=p(x|y)p(z|y)$
inverse Fork Structure(v-structure, collider, head-to-head, immoralities)

$p(x,y,z)=p(x)p(z)p(y|x,z)$
Q : X와 Z가 독립인가?
A : Yes!
Why?
$p(x,y,z)=p(x)p(z)p(y|x,z)$
$\frac{p(x,y,z)}{p(y|x,z)}=p(x)p(z) \rightarrow p(x,z)=p(x)p(z)$

Q : Y가 주어졌을 때 X와 Z가 조건부 독립인가?
A : NO!
Why?
$p(x,z|y)=\frac{p(x,z,y)}{p(y)}=\frac{p(x)p(z)p(y|x,z)}{p(y)}$
베이즈 정리에 의해
$p(x|y)=\frac{p(x)p(y|x)}{p(y)}$
$p(z|y)=\frac{p(z)p(y|z)}{p(y)}$
처럼 나타낼 수 있다.
$p(x,z|y)=p(x|y)p(z|y)$가 되면 조건부 독립임을 알 수 있다.
$p(x|y)p(z|y)=\frac{p(z)p(y|z)}{p(y)}\frac{p(x)p(y|x)}{p(y)}=\frac{p(x)p(z)p(y|z)p(y|x)}{p(y)p(y)}$
조건부 독립이 되려면 $p(y|x,z)=\frac{p(y|z)p(y|x)}{p(y)}$가 되어야 하지만, 두 식은 같지 않기 때문에 조건부 독립이 아니다!
정리하자면 다음 표와 같다.
Chain Structure Fork inverse Fork
| $X\perp Z$ | NO | NO | Yes |
| $X\perp Z|Y$ | Yes | Yes | Yes |


그럼 다음과 같은 예제를 풀어보자

Q : $W\perp X|Y?$
A : No!
Why?
표를 보면 위 그림은inverse Fork 형태에서 $X\perp Z|Y$형태와 같음

Q : $W\perp X|Z?$
A : NO!
Why?
표에서처럼 W와 X는 독립인 것 같지만, 사실 이 형태는 $X\perp Z|Y$형태와 같음. 왜냐하면 Z는 Y에 대한 정보를 받고 있기 때문에! 따라서 W와 X는 조건부 독립이 아니다!
이해가 잘 안된다면 아래 그림을 참고하자
Bayes ball이 굴러가는 경로라고 보면 된다. 경로가 끊이지 않는다면 독립이 아니라고 생각하면 된다.
왼쪽 그림은 독립 , 오른쪽 그림은 Z가 주어졌을 때 독립이 아님! Bayes ball이 W에서 X로 잘 굴러가기 때문!
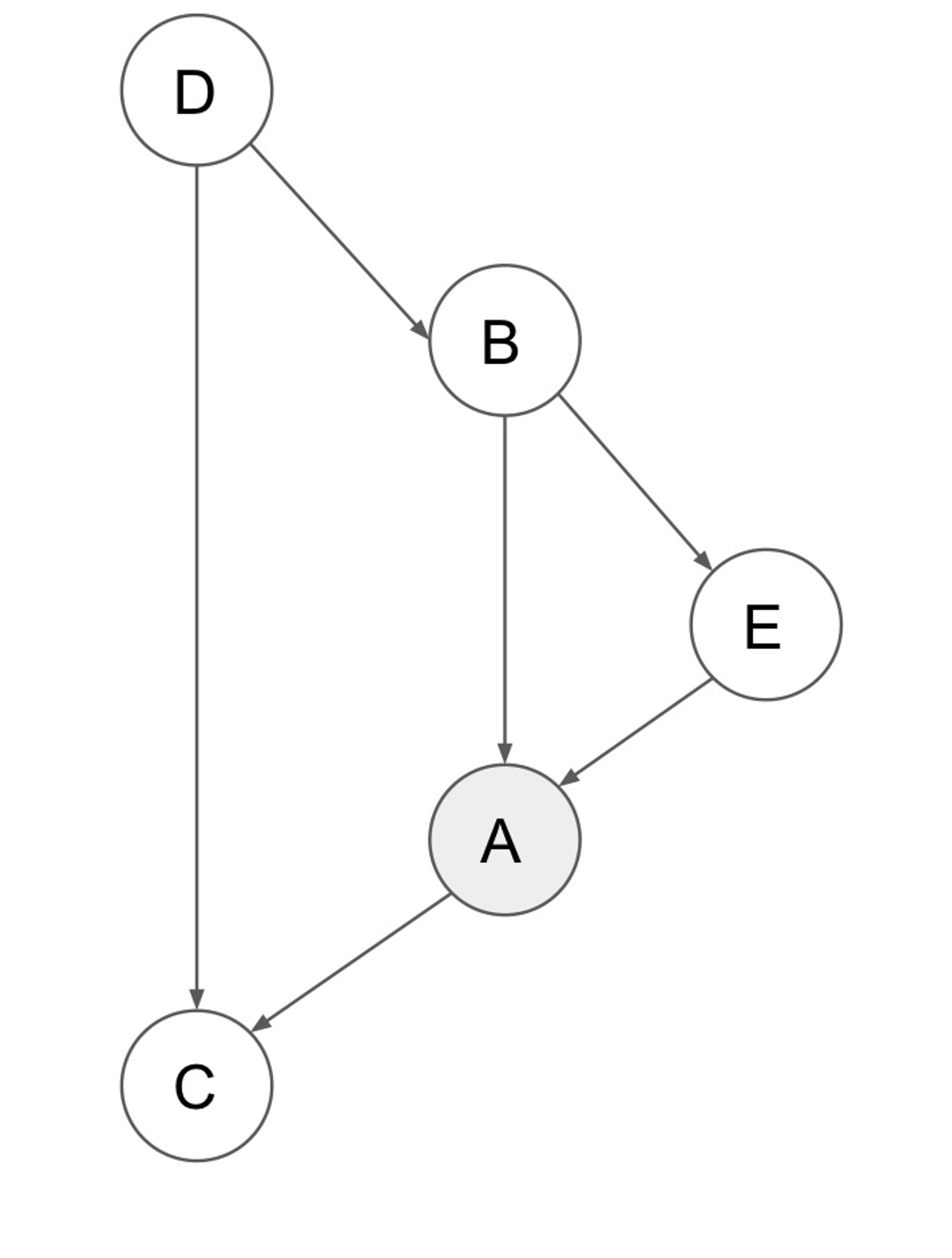
Q : 이 그림에서 A가 주어졌을 때 C와 E는 독립인가?
A : NO!
Why?
우선 이 그림에서 Chain structure 형태가 보인다.( E → A → C) 이 형태를 보고 바로 독립이라고 생각할 수 있다.(경로가 끊겨있기 때문에)
하지만 이 그림에서 E → C로가는 경로가 한 가지 더 있다. 바로 C ← D → B →E 이렇게 말이다.
이 형태를 보면 Fork의 형태와 같다. Fork는 경로가 끊이지 않았기 때문에 C에서 E까지 굴러갈 수 있다. Bayes ball이 굴러간다는건 독립이 아닌 것이라는 것과 같음!! 그렇기 때문에 NO!
마지막으로 PC algorithm에 대해서 정리하고 마치겠습니다.
PC Algorithm
PC 알고리즘은 베이지안 네트워크의 구조를 학습하는데 사용됩니다. 이 알고리즘을 통해 변수 간 조건부 독립성을 추론하고, 이를 통해 인과관계를 유추합니다. PC 알고리즘의 Step은 다음과 같습니다.
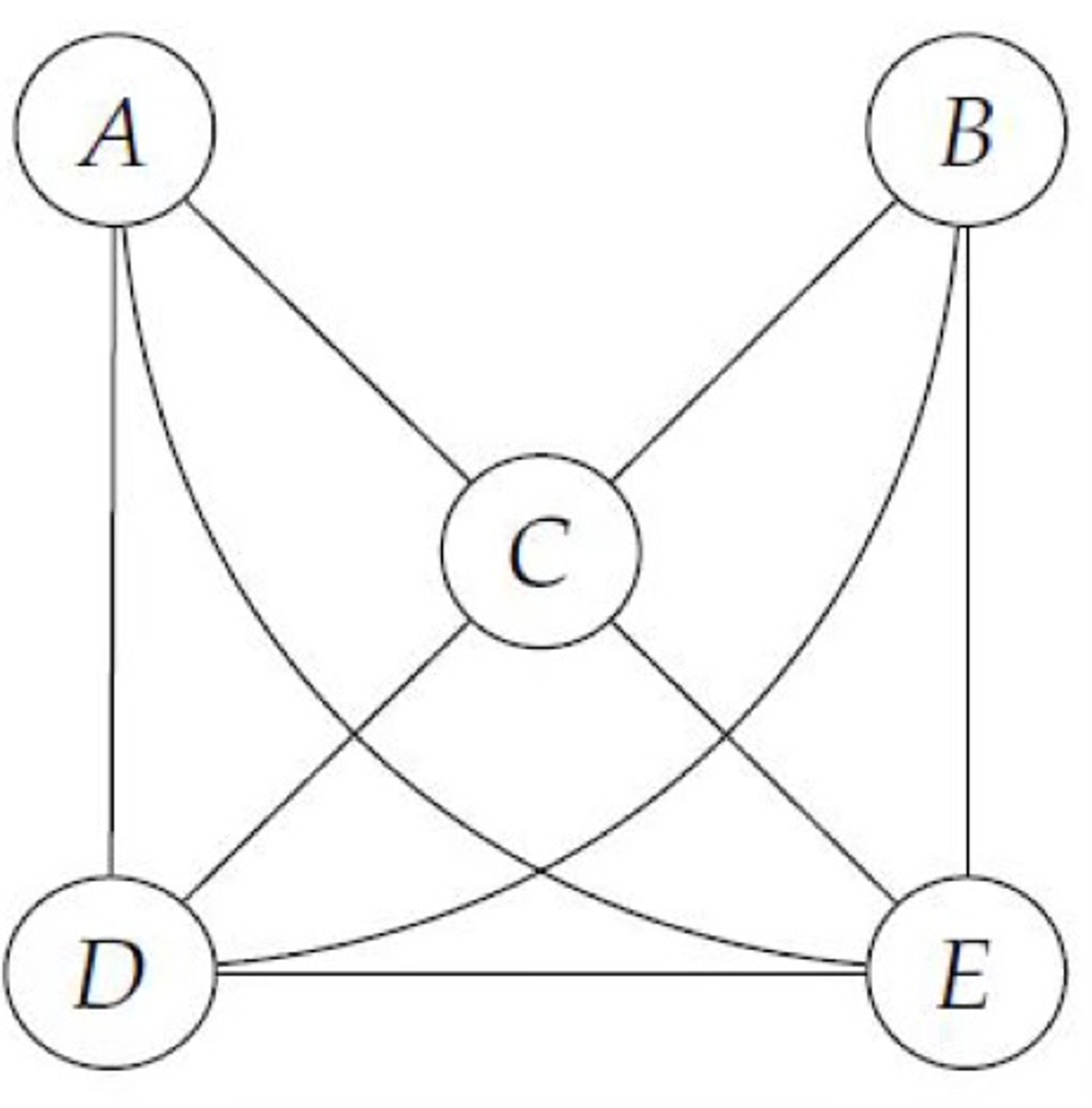
아래 그래프의 관계를 추론하고 싶다고 하겠습니다.(True causal Graph)

1. 모든 변수들 사이 존재하는 Edge(선)를 그려줍니다.

2. 관계가 없는 즉, 독립 관계인 노드의 Edge를 제거해 줍니다.( True graph에서 보면 A와 B는 v-structure 구조를 가지기 때문에 독립인 것을 알 수 있습니다.)
위 그림에선 A와 B가 독립이 되어 두 개의 노드 사이의 Edge를 제거합니다. 또한 조건부 독립이라면 그때 또한 역시 Edges를 제거합니다. 이를 반복하여 Edges를 제거하게되면 아래 그림과 같이 됩니다. (예시 : Chain structure인 A→C→E에서 C가 주어지면 A와 E는 독립이므로 A와 E를 직접적으로 연결짓는 선은 제거)

3. A와 B가 독립이므로 A,B,C에서는 v-structure 구조를 가지고 있다고 생각할 수 있습니다.

4. 마지막으로 D와 E에도 방향을 그려줘야 하는데, 나머지 방향에서는 v-sturcture가 되지 않도록 방향을 설정해주어야 합니다. 결과는 다음과 같습니다.

감사합니다.
'머신러닝' 카테고리의 다른 글
| [머신러닝] 유전 알고리즘(Genetic Algorithm) (1) | 2024.09.13 |
|---|---|
| [머신러닝] SMOTE(Synthetic Minority Over-sampling Technique) (1) | 2024.09.13 |
| [머신러닝] Oversampling & Undersampling (0) | 2024.09.11 |