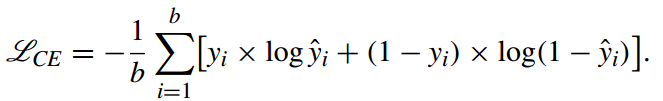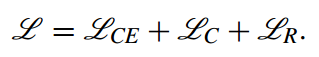이번 글에서는 2023년 5월 International Journal of Machine Learning and Cybernetics 저널에 게재된 OUBoost 논문에 대해 작성하겠습니다.

Abstract

현실 세계에서는 종종 불균형 데이터가 발생하며, 이는 다수 클래스를 잘 예측하지만 소수 클래스에 대해 분류기가 편향되어 예측 정확도가 떨어지는 문제를 야기합니다.

이 논문에서는 Peak clustering 방법을 사용해 다수 클래스의 데이터를 선택하여 undersampling을 수행하는 새로운 기술을 제안합니다. 또한, 소수 클래스에 대해 SMOTE 기반의 synthetic 데이터를 생성하고, 이를 부스팅 알고리즘과 결합한 새로운 OUBoost 알고리즘을 제시했습니다.

30개의 실제 불균형 데이터셋에 대해 여러 평가 지표를 사용하여 실험을 진행했으며, 대부분의 데이터셋에서 OUBoost를 사용했을 때 소수 클래스의 예측 성능이 개선되는 것을 확인했습니다.

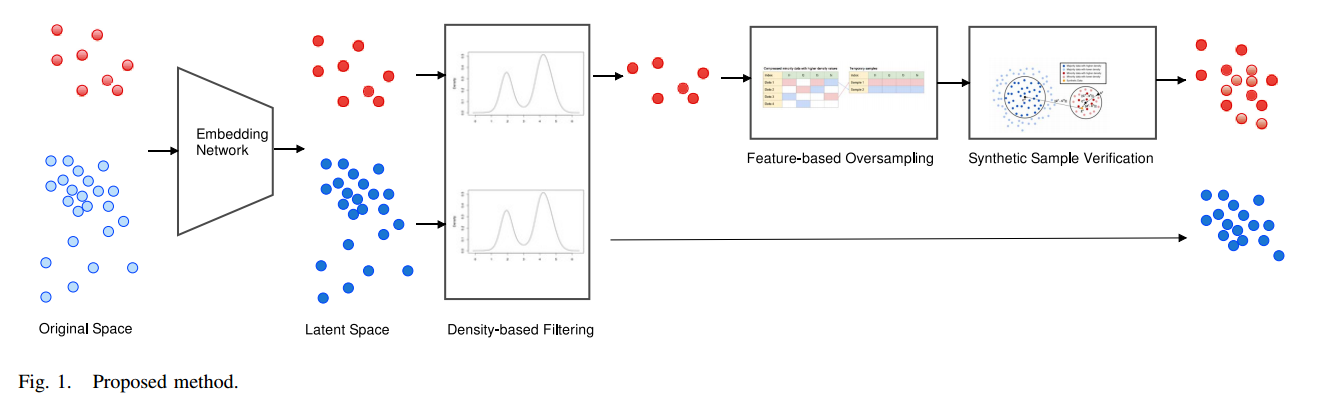
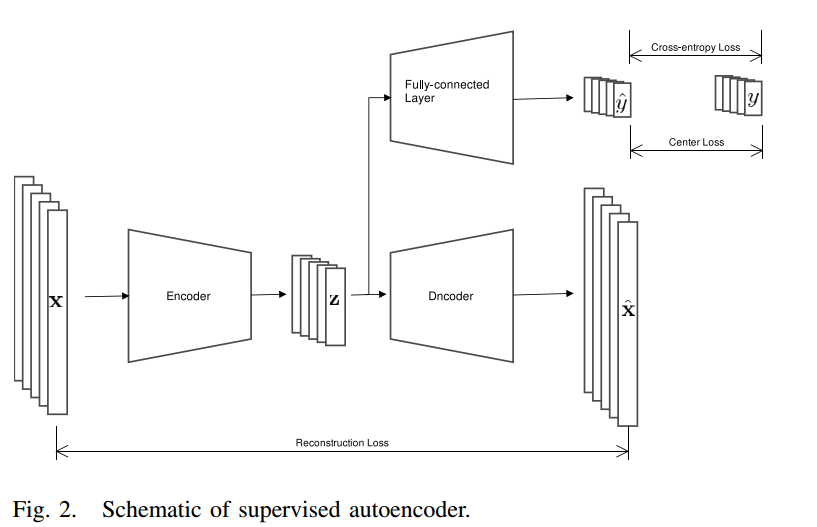
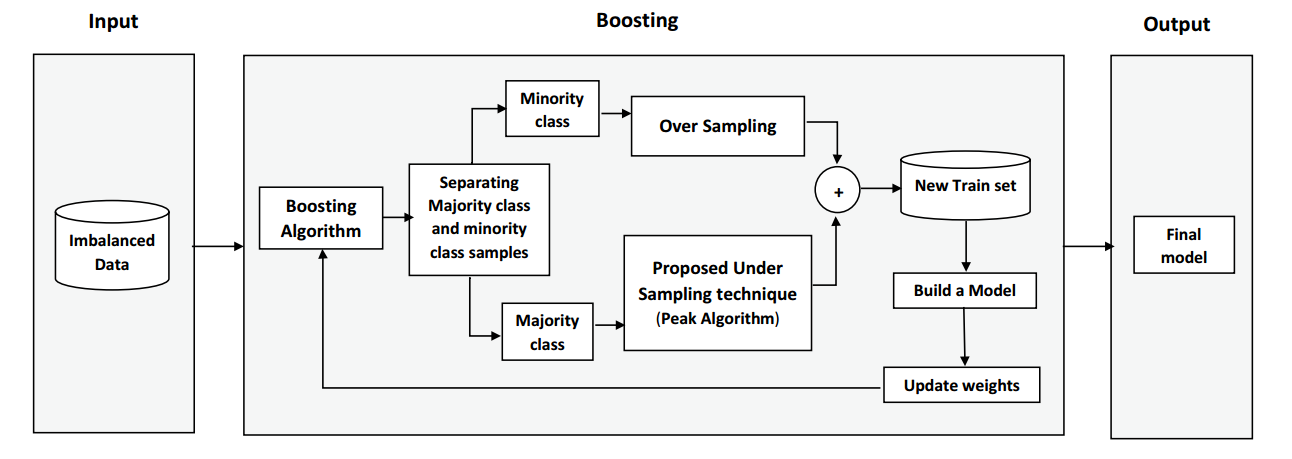
아래 사진은 OUBoost 모델의 아키텍쳐입니다.

Density-peak clustering

이 논문에서 Density-peak clustering(DPC)방법을 사용하여 다수 클래스 데이터를 제거하였는데, DPC가 무엇인지 살펴보겠습니다.

Density-peak clustering (DPC) 알고리즘은 복잡한 구조를 가진 데이터셋에서 클러스터를 식별하기 위해 설계된 클러스터링 알고리즘입니다. 클러스터의 중심을 식별하기 위해 크게 2가지 과정을 거치게 됩니다.

1. 클러스터 중심은 local density가 낮은 샘플들 사이에 위치하며, 더 높은 밀도를 가진 샘플들로부터 상대적으로 멀리 떨어져 있습니다.
2. 샘플 간의 거리와 local density를 결합하여 클러스터를 정의합니다.

여기서 local density, distance라는 2가지 지표가 클러스터를 정의하는데 사용되기 때문에 각각의 정의들을 살펴보겠습니다.

local density($\eta_i$) : 샘플 j주변에 있는 샘플의 개수를 나타냅니다. 이는 반경 $t_r$ 내에 있는 이웃 샘플 수로 정의됩니다.

$\eta_j = \sum_{k \in S, k \neq j} \Omega(d(j, k) - t_r),$

$d(j,k)$ : 샘플 j와 k간의 거리

$t_r$ : 샘플 주변의 밀도를 결정하기 위한 임계값

$\Omega(y) =\begin{cases}1, & \text{if } y < 0, \\0, & \text{otherwise.}\end{cases}$

만약, 샘플 주변에 데이터가 많으면 $\Omega$값은 음수가 되므로 1을 출력하게 됩니다. 즉, 주변에 데이터가 많을수록 $\eta$값이 커집니다. (보통 클러스터 중심 주변에 데이터가 많이 모이게 되죠! 그러니까 $\eta$가 크다는 건 클러스터의 중심일수도 있다는 것입니다!)

최소 거리($\mu_j$) :더 높은 local density를 가진 샘플들로부터의 최소 거리를 계산합니다. 단, local density가 가장 높은 샘플의 경우, 이는 다른 모든 샘플로부터의 최대 거리로 정의됩니다.

$\mu_j = \begin{cases} \max \{d(j, k) \mid k \in S\}, & \text{if } \eta_j \geq \eta_k \text{ for all } k \in S, \\\min \{d(j, k) \mid \eta_j < \eta_k, k \in S\}, & \text{otherwise}.\end{cases}$

위 과정을 통해 각 데이터 포인트에 대해 $\eta_j$, $\mu_j$를 각각 구하여 클러스터의 중심을 결정합니다.

클러스터 중심

각 샘플의 Density와 Distance를 결합하여 새로운 값 $\lambda_j$를 계산합니다.($\lambda_j=\mu_j*\eta_j$)

$\lambda_j$ 값을 내림차순으로 정렬하고, 높은$\lambda_j$ 값을 가진 샘플을 클러스터 중심으로 선택합니다.

클러스터 할당

클러스터 중심이 결정된 이후, 나머지 샘플들은 가장 가까운 클러스터로 할당되게 됩니다.

$\Psi_j = \begin{cases} j, & \text{if } \eta_j \geq \eta_k \text{ for all } k \in S, \\\arg\min \{d(j, k) \mid \eta_j < \eta_k\}, & \text{otherwise}.\end{cases}$

예를 들어 설명해보겠습니다.

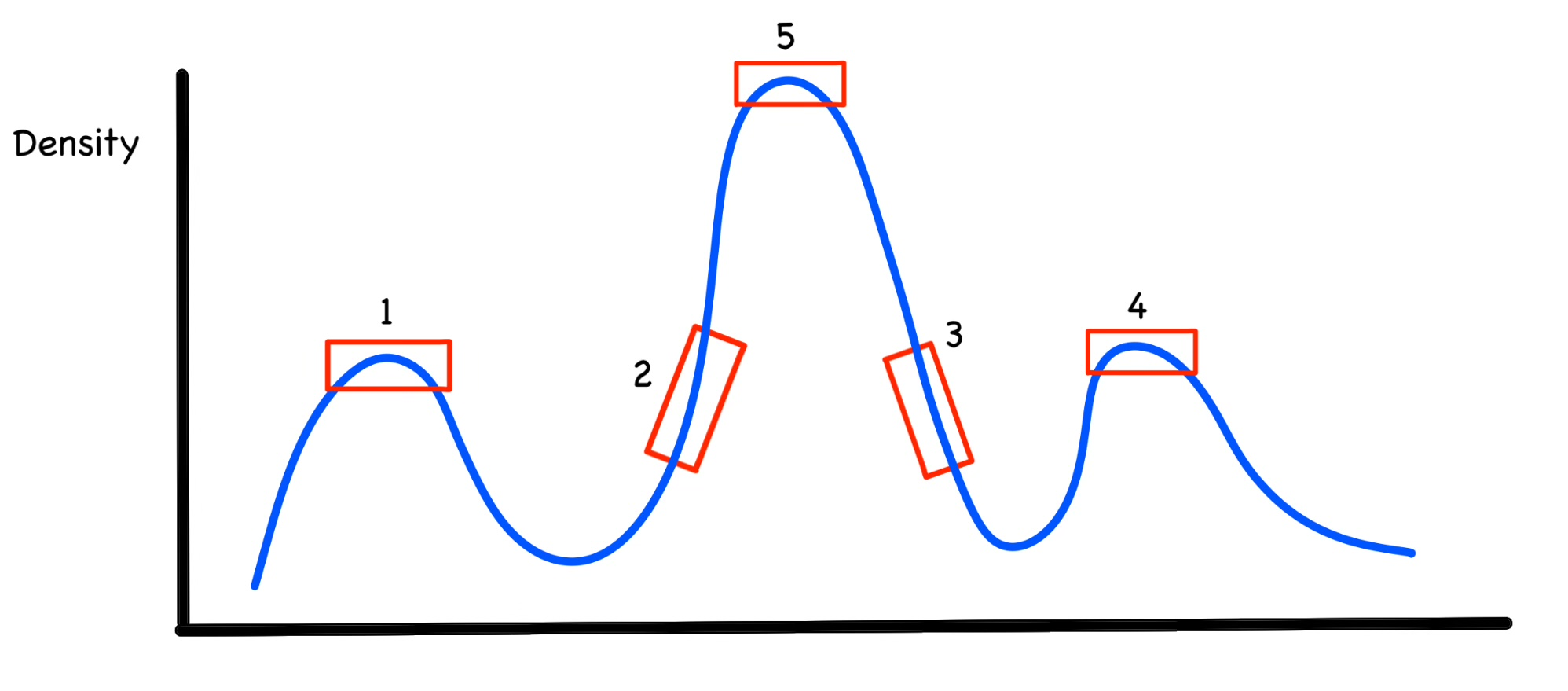
위 사진은 $\eta_1=\eta_2=\eta_3=\eta_4$(1~4번까지 같은 density를 가지고, 5는 다른 Density를 가진다)라고 가정하겠습니다.

그렇게 되면 $\lambda$를 계산하기 위해 최소 거리 $\mu$를 계산해야 합니다.(2번,3번 다음의 포인트가 바로 저 네모난 박스라고 하고 거리를 계산하겠습니다. 저 네모난 두 박스는 1,2,3,4보다는 Density가 더 높음)

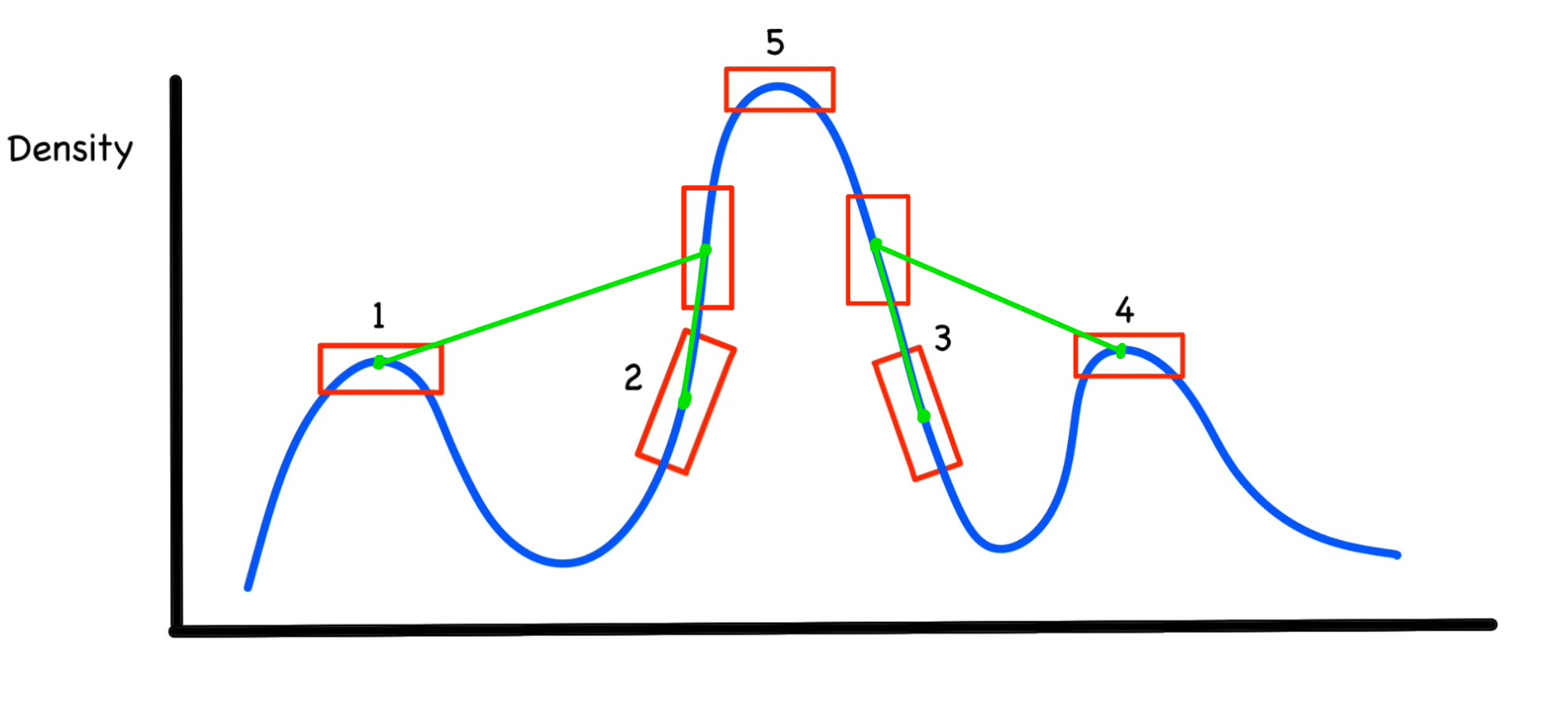
$\mu_1,\mu_2,\mu_3,\mu_4$를 위의 식에 대입해보면 초록색 선이 거리가 될 것입니다. 1,2,3,4에 대해서 계산해보면 대략 $\mu_1,\mu_4,\mu_2,\mu_3$ 이 순서로 클 것 같습니다.(최소 거리를 계산해야하기 때문에 1,4번은 거리가 멀고 2,3번은 가까운 것을 알 수 있습니다!)

클러스터의 중심을 계산하기 위해 $\lambda$를 계산하게 되면 $\lambda_5,\lambda_1,\lambda_4,\lambda_2,\lambda_3$이 순서로 될 것이고 아마도 더 많은 샘플에서 수행하게되면 클러스터의 중심인 1,3,5만 클러스터링이 될 것 입니다! 그리고 나서 나머지 샘플들은 1,3,5 클러스터에 더 가까운 곳으로 할당이 된다고 생각하시면 됩니다!

Proposed Peak-based Undersampling Algorithm

이제는 DPC 알고리즘을 살펴보았으니 이 알고리즘을 통해 어떻게 Undersampling을 수행했는지 살펴보도록 하겠습니다.

1. 다수 클래스 데이터에 DPC 알고리즘을 적용시켜 e개의 클러스터 생성
2. 각 클러스터의 중심에서 소수 클래스와의 거리와 밀도를 계산
3. 새로운 측정값 $H_i$를 사용하여 다수클래스에서 가장 효과적인 샘플을 선택
   1. $H_i​=u×dens_i​+v×dist_i​,\ \ \ \ \ where \ \ \ \ \ u+v=1$
      1. $dens_i = \sum_{j \in \text{cluster}_i} \eta_j$
      2. $dist_i = \sum_{q \in \text{minclass}} d(p, q)$ $p : centroid\ of\ cluster_i$
4. $H_i$값이 높은 샘플 중 서로 너무 가깝지 않은 샘플을 선택합니다.
   1. 선택 기준은 $L = \{ x_i \mid x_i, x_j \in H \text{ and } d(x_i, x_j) > \theta \}$
5. 선택된 샘플과 Minority class data를 병합해 수정된 데이터셋을 생성합니다. 이 데이터는 여전히 불균형 하지만, 원본 데이터보다는 불균형 비율이 낮습니다.(아마 분류기를 계속 학습하면서 불균형이 완화될 것이라 보입니다.)

Proposed OUBoost Algorithm

이제 저자가 제안한 OUBoost 알고리즘의 전체 흐름을 살펴보겠습니다. 위에는 Undersampling을 위한 방법론을 소개했지만, OUBoost는 소수 클래스를 SMOTE를 사용해 데이터 생성하기 때문에 두 기법을 결합하여 알고리즘이 어떻게 진행되는지 살펴보겠습니다!

1. 데이터셋 분리 및 오버샘플링
   1. 원본 데이터셋 S를 소수 클래스와 다수 클래스로 나눕니다.
   2. SMOTE를 사용하여 소수 클래스에서 합성 데이터를 생성하고 이를 원본 데이터셋에 추가합니다.
2. 다수 클래스 언더샘플링
   1. 제안된 Peak 기반 언더샘플링 알고리즘을 사용하여 다수 클래스에서 샘플을 선택합니다.
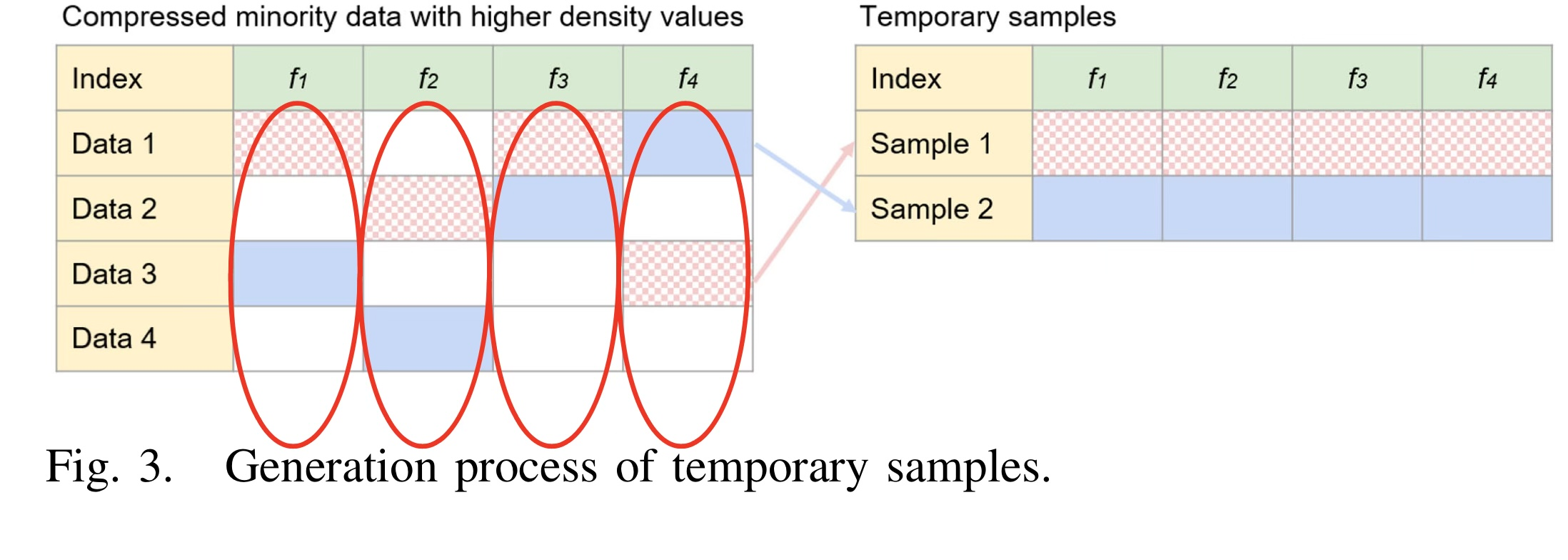
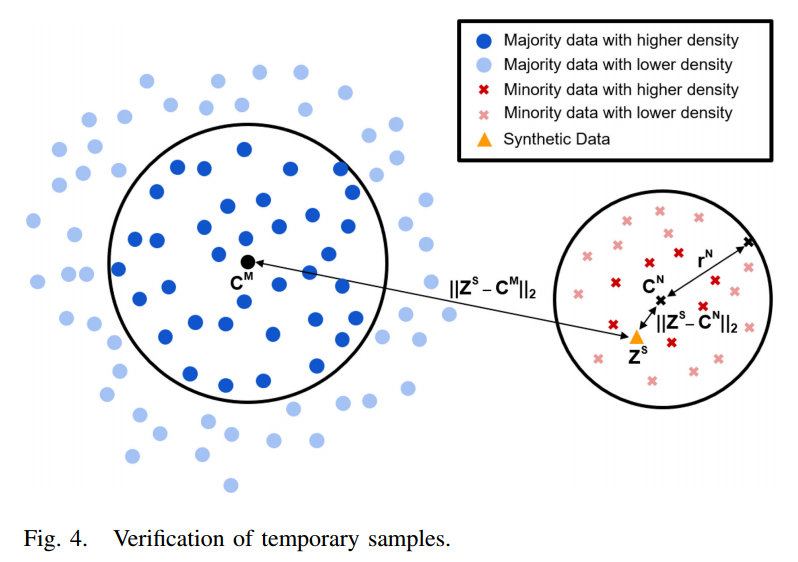
3. 임시 데이터셋 생성
   1. 소수 클래스의 모든 샘플과 다수 클래스에서 선택된 샘플을 결합하여 새로운 임시 데이터셋 $S'_t$을 만듭니다.
   2. 이 데이터셋은 각 부스팅 단계에서 약한 학습기(weak learner)를 훈련하는 데 사용됩니다.
   3. 이때 불균형 비율이 되도록 임시 데이터셋 생성(불균형 비율은 우리가 선택할 수 있음)
      1. 만약 불균형 비율이 2:1이라고 하면, 생성된 소수 클래스의 데이터 수와 제거되고 남은 다수 클래스 데이터 수의 비율이 2:1이 되도록 데이터 정제
4. 가중치 업데이트 및 반복
   1. 각 단계에서 약한 학습기의 예측 오류율 $\epsilon_t$을 계산합니다.
   2. 오류율을 기반으로 가중치 업데이트 매개변수 $\alpha_t$를 계산 $\alpha_t=\frac{\epsilon_t}{1-\epsilon_t}$
   3. 데이터셋 S의 각 샘플에 대해 가중치를 업데이트하고 정규화합니다.
5. 최종 모델 생성
   1. T번의 반복 후, 최종 모델은 각 약한 학습기의 투표 결과를 기반으로 결정됩니다
      1. $H(x) = \arg\max_{y \in Y} \sum_{t=1}^{T} h_t(x, y) \log \frac{1}{\alpha_t}$

Results

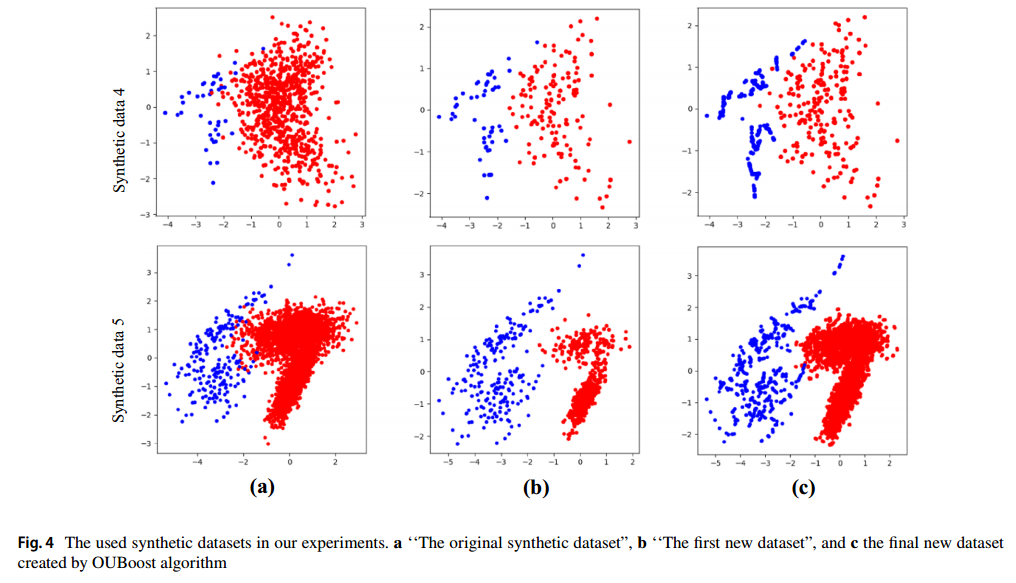
위 그림은 OUBoost 과정이 진행되면서 데이터 생성, 제거 과정을 표현한 그림입니다. (빨간색 : 다수 클래스, 파란색 : 소수 클래스)

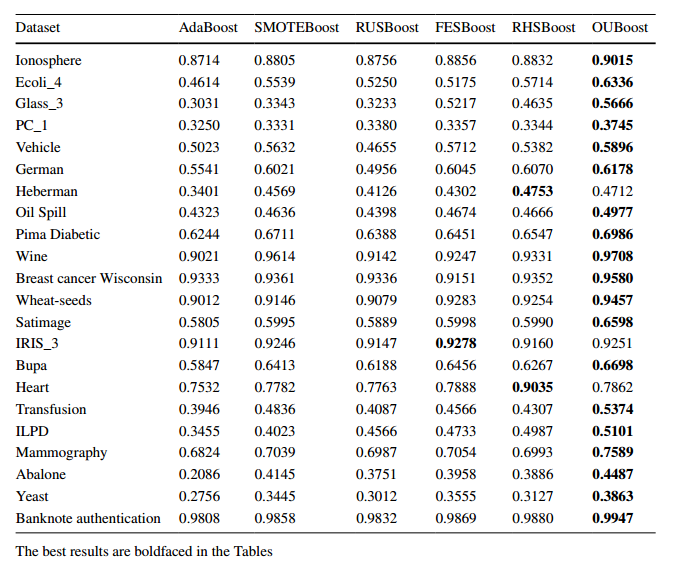
실제 불균형 데이터에 대해서 OUBoost를 적용한 모델과 다른 모델들에 대해서 F-score를 비교해보았습니다. 대부분의 경우 OUBoost의 성능이 우수한 것을 볼 수 있었습니다.

불균형 상황에서 잘 분류할 수 있다는 것은 큰 강점인 것 같습니다. 제조, 금융, 의료업에서는 아주 도움이 되는 모델이라고 느꼈습니다.

감사합니다.

참고문헌

1. OUBoost : https://link.springer.com/article/10.1007/s13042-023-01839-0

이번 게시글에서는 2022년에 IEEE에 발표된 Learning From Imbalanced Data With Deep Density Hybrid Sampling 논문을 다뤄보겠습니다.

Abstract

Imbalaced data 문제를 해결하기 위해서 많은 방법들이 있었는데, 대부분의 방법들은 오직 minority, majority class에 대해서만 고려하고 그 두개의 클래스 간의 관계에 대해서는 고려하지 않고 있습니다.

게다가 데이터 생성하는 많은 방법들이 original feaure space로부터 데이터를 생성하고 있으며 이때 Euclidean distance를 사용합니다(SMOTE처럼). 하지만, high dimensional space일수록 Euclidean distance는 더이상 중요한 거리가 되지 않습니다. 그래서 저자는 새로운 방법론인 DDHS(deep density hybrid sampling)방법을 소개하며 불균형 문제를 해결하고자 합니다.

저자가 기존의 방법론들과 어떻게 다르게 접근하여 불균형 문제를 해결했는지 살펴보도록 하겠습니다.

Proposed Method

많은 Data-level 방법들이 SMOTE를 응용한 방법이지만, 크게 2가지 문제를 가져온다고 합니다.

1. 오직 MInority samples만 고려하고, Majority class가 가져오는 영향을 무시한다
2. Nearest neighbors를 찾기 위해 Euclidean distance(SMOTE에선 이 거리를 사용함)를 사용하지만, high-dimensional datasets에서는 정확하게 측정할 수 없다.

이 문제를 해결하기 위해 저자는 어떻게 해결하려고 했는지 살펴보겠습니다.

위 사진은 저자가 제안한 모델의 아키텍쳐입니다. 이 부분을 하나하나씩 살펴보도록 해서 어떻게 Oversampling, Undersamplilng을 수행했는지 확인해보도록 하겠습니다.

Notation

위 과정을 진행하기 전에 Notation에 대해 정의하고 수행하겠습니다.

$\{(x_i,y_i)^m_{i=1}\}, where \ x_i \in \mathbb{R}^D$

$x_i$ : feature vector

$y_i$ : corresponding label

$m$ : the number of training examples

$z_i$ : $x_i$에 의해 projection된 벡터 $z_i \in \mathbb{R}^d$

이때 d<D ($x_i$를 저차원 $z_i$로 사영시켰으므로 D가 d보다 큰것은 자명합니다.)

이 작업은 binary classification 작업에 초점이 맞춰져 있습니다.

Embedding Network

저자는 제안된 방법을 develop하기 위해 autoencoder를 활용하였습니다.

Original autoencoder의 구조는

1. Encoder
   1. 원본 데이터를 latent space으로 변환시키는 네트워크
2. Decoder
   1. latent vector들을 원본 데이터로 복원하는 네트워크

이렇게 2가지로 구성되어있습니다.

목표는 reconstruction loss를 최소화함으로써 Encoder와 Decoder를 동시에 최적화 하는 것입니다.

$x$ : 원본데이터

$D(E(x))$ : 원본데이터를 Encdoer를 통해 latent space로 축소시키고 다시 디코더를 통해 원본데이터의 차원으로 복원한 데이터

지도학습의 경우, 훈련 과정에서 레이블 정보를 활용하면 예측 성능을 향상시킬 수 있습니다. 이는 모델이 class 근접성을 유지하면서 동일한 클래스의 샘플들이 잠재 공간에서 더 가까워지도록 학습하는 데 도움이 됩니다. 따라서, 저자는 총 3가지 손실 함수를 사용하여 이러한 효과적인 학습을 달성하려고 합니다.

아래 그림은 저자가 제안한 방법의 아키텍쳐입니다.

3가지 손실함수는 다음과 같습니다.

1. Reconsturction loss

• Autoencoder에 의해 계산이 되고, 이때 MSE(mean square error)를 사용하여 loss를 계산하게 됩니다.

$x_i$ : original data point(원본 데이터)

$\hat{x_i}$ : reconstructed data point(복원된 데이터)

$b$ : batch size(배치 사이즈)

실제 데이터와 Encoder, Decoder를 거쳐서 복원된 데이터간의 차이가 어느정도인지 MSE를 통해 계산되어 이 loss가 최소가 되도록 업데이트 됩니다.

2. Cross-entropy loss

• 또한 저자는 Cross-entropy loss를 제안했는데, 레이블 정보를 활용하여 클래스가 다른 데이터들간의 거리는 멀게, 클래스가 같은 데이터들간의 거리는 가깝게 하는것이 목적입니다!

이렇게 loss를 설정함으로써 부정확한 클래스로 분류된 데이터에 대해서 패널티를 부과하여 loss를 계산하게 됩니다.

3. Center loss

• 마지막 손실함수는 Center loss함수입니다. 말 그래도 Class Center로부터 멀어질수록 패널티를 부여하게 됩니다. 그래서 이 loss를 통해서 같은 클래스들끼리 center로 향하도록 하는것이 목적입니다.

$c_{y_i}$ : latent space에서 $y_i$클래스의 center

$z_i$ : latent vector

이 3가지 loss 함수를 통해서 projected data point들이 latent space에서 separable하게 하는 것이 목적입니다. latent space는 original feature space보다 저차원이기 때문에 high dimensional space에의해 발생되는 문제를 완화할 수 있습니다.

최종 loss는 다음과 같습니다.

Density-Based Filtering

Embedding network훈련 과정이 완료된 후 저자는 high-quality datapoint를 선택하기 위한 기준으로써 density를 사용합니다.

• Low-density data들은 다른 data point들과 멀이 떨어져 있기 때문에 noise가 될 수 있고,
• High-density data들은 cluster를 대표할 가능성이 큽니다.

저자는 이 part에서 high-density에 존재하는 data point에 대해 정의하고자 합니다.(어떤 기준으로 data가 high, low density에 속하는지)

저자는 latent space에서 데이터들의 density를 추정하기 위해 KDE(Kernel Density function)을 사용합니다. 그 중 Gaussian kernel을 사용하여 density를 추정하고자 합니다.

아래 링크는 kernel density function에 대해서 자세하게 다뤄주신 블로그 글입니다. 자세하게 설명해주셔서 궁금하신 분들은 확인해보시길 바랍니다!

https://darkpgmr.tistory.com/147

이제 density를 majority, minority class에 대해서 추정하려 합니다.

• Majority class
  • majority density $Q_2$의 quartile보다 큰 data들만 유지시키도록 합니다.
• Minority class
  • minority density $Q_3$의 quartile보다 큰 data들만 유지시키도록 합니다.

훈련 과정에서 데이터의 25%만을 유지하며 oversampling을 수행하지만, 나머지 75%의 데이터를 완전히 버리는 것은 아닙니다. 이 데이터는 나중에 classifier 훈련 과정에 포함될 예정이며, 특히 majority 데이터의 50%는 undersampling 과정에서 삭제됩니다.

이런 이유때문에 hybrid sampling인 것 같네요.

Generation of Synthetic Samples

위 그림은 데이터 생성하는 방법입니다. Minority class를 oversampling 하는 법에 대해 설명하도록 하겠습니다.

아래 그림은 4개의 latent vector가 존재하고, 4개의 DATA가 존재한다고 가정하고 있습니다.

저자는 다양한 synthetic samples를 생성하기 위해 feature-level sampling 기법을 제안합니다.

위 그림을 예시로 들어서 설명하겠습니다. (latent feature은 4개)

Minority class에서 선택된 샘플들의 latent feature 집합 $V=[v_1,v_2,...,v_4]$이 주어지면, 각 feature의 value set이 정의됩니다.

• 먼저, 첫 번째 latent feature $v_1=[v_{11},v_{21},...,v_{41}]$(빨간색 원)에서 하나의 값을 무작위로 선택(복원 추출)하여 synthetic sample을 생성하기 시작합니다.
• 동일한 방식으로 나머지 feature2,3,4 들도 순차적으로 선택해 synthetic sample을 생성합니다.

랜덤한 process로 진행되기 때문에 생성되는 samples의 다양성을 높일 수 있습니다.

Verification of Synthetic Samples

Generation process가 완료되면, 생성된 샘플들이 좋은 퀄리티를 가지고 있는지 평가해볼 필요가 있습니다.

좋은 데이터가 생성됐는지에 대한 평가 기준은 density를 사용하게됩니다.

아래 사진은 각각에 대한 Notation입니다.

그리고 아래 사진에는 좋은 데이터가 생성됐는지에 대한 기준입니다.

위의 식을 보면 생성된 데이터가 Majority class의 center보다 Minority class의 center보다 가까운지 확인하는 것입니다. 즉, Minority class의 데이터를 oversampling 했으니 생성된 데이터는 Minority class의 center보다 가까워야겠죠? 그래서 저 조건이 성립해야 합니다.

또한 두번째 식을 보면 생성된 샘플과 Minority class의 거리가 center Minority class의 반지름보다 작아야 합니다. 조금 더 high-quality를 가진 샘플이 생성되어야한다는 조건을 추가로 만든 것 같습니다.

이렇게 두가지 식의 조건을 만족하면 좋은 퀄리티를 가진 데이터가 생성되었다고 볼 수 있습니다.(근데 사실 2번째 식만 만족하면, 첫번째 식은 자동으로 만족되는 것 같은데 굳이 첫번째 식이 필요한가?라고 생각해봤습니다….)

Experimental Results

저자가 데안한 모델을 다른 Data-level algorithm과 비교해서 성능이 어떤지 확인해보겠습니다.

Linear SVM을 사용하여 AUC와 AUPRC를 측정하였습니다.

• AUC

• AUPRC

저자가 제안한 모델이 대체적으로 좋은 성능을 가지는 것을 확인할 수 있습니다.

또한 Embedding Network에서 사용된 Loss functino에 대해서 Ablation studies를 진행한 결과입니다.

역시 3가지 loss를 사용하면 좋은 성능이 나타나는걸 확인할 수 있습니다

• cross-entropy loss가 분류기가 제대로 분류하면 loss가 작아지고, 못하면 loss가 커지기 때문에 만약 binary classification 에서 분류기가 분류를 더 잘한다면 더 좋은 성능을 가질 수 있지 않을까?라는 생각이 듭니다!

감사합니다.

참고문헌

1. [논문] https://ieeexplore.ieee.org/document/9723474

Imbalanced data

이 게시글에선 Imbalaced data 상황에서 해결할 수 있는 Oversampling과 Undersampling의 개념에 대해서 다뤄보겠습니다.

우선, Oversampling과 Undersampling 기법이 왜 필요한지부터 생각해 볼 필요가 있습니다.

Classfication문제에서 majority class(다수 클래스) data가 minority class(소수 클래스) data의 수보다 훨씬 많은 경우, 모델은 new data(minority class data)에 대해서 주로 majority로 분류하게 되는 경향이 있습니다. 이렇게 되는 경우는 모델이 정확도를 최대화하려고 할 때 발생하게 됩니다.

아래 예시를 들어보겠습니다. 아래와 같이 불량 정상을 예측하는 모델이 있다고 가정하겠습니다.

위 표를 보면 이 모델의 정확도는 $\frac{1+979}{1+11+9+979}=\frac{980}{1000}$=0.98입니다. 이 모델은 좋은 모델이라고 할 수 있을까요? 사실 이 모델은 정확도는 되게 높지만, 좋은 모델이 아니라고 볼 수 있습니다. 만약 minority class의 예측을 중요시하게 되는(예를 들어 암과 정상 데이터) 데이터의 경우에는 전혀 도움이 되지 않는 모델입니다. 그래서 이런 Imbalacend data 문제를 해결하기 위해서 Oversampling과 Undersampling이 필요하게 됩니다. 이제 Oversampling과 Undersampling에 대해서 다뤄보겠습니다.

Oversampling

Oversampling은 minority class(소수 클래스)의 data를 복제하거나 증가시켜 majority class(다수 클래스)와의 균형을 맞추는 방법입니다. 이를 통해 모델이 minority class에 대해 더 나은 성능을 나타낼 수 있도록 합니다. Oversampling 기법은 Minority class의 data의 수가 현저히 적을 때 유용하게 사용될 수 있습니다. (위 방법의 경우에는 Minority class의 data를 무작위로 복제하여 샘플 수를 늘리는 방법)

장점(Pros)

1. 소수 클래스 데이터를 효과적으로 늘려 모델이 소수 클래스에 더 민감하게 반응할 수 있도록 함(모두 다수 클래스로 예측하는 문제를 해결할 수 있음)
2. 구현이 간단하고 빠름

단점(Cons)

1. 데이터를 단순하게 복제하기 때문에 과적합(Overfitting)이 될 수 있음

Undersampling

Undersampling은 majority class(다수 클래스)의 data를 줄여 minority class(소수 클래스)와의 균형을 맞추는 방법입니다. 다수 클래스의 데이터가 많을 때 학습 데이터에서 다수 클래스의 샘플을 무작위로 선택해서 그 수를 줄이는 방법입니다.

장점(Pros)

1. 간단하고 빠르며 데이터 셋의 크기가 줄어들어 학습 시간이 단축됩니다.

단점(Cons)

1. 다수 클래스의 데이터를 랜덤으로 선택하여 개수를 줄였기 때문에 다수 클래스의 정보가 손실될 수 있습니다. 그로 인해 모델 성능도 저하가 될 수 있습니다.(모델이 다수 클래스의 중요한 패턴을 학습하지 못할 수 있음)

데이터가 불균형한 상황에서 데이터를 증강시키거나 줄여서 모델의 성능을 향상시킬 수 있도록 하는 Sampling 기법을 다뤄보았습니다. 이 기법들로 인해 불균형한 상황에서 조금 더 중요한 클래스에 대해서 초점을 맞출 수 있습니다.

Oversampling과 Undersampling에는 다양한 기법이 존재하기 때문에 다른 게시글에서 응용기법을 포스팅하도록 하겠습니다.