이번 글에서는 유전 알고리즘에 대해 다뤄보도록 하겠습니다.
유전 알고리즘
유전 알고리즘(Genetic Algorithm)은 주로 복잡한 문제에서 최적의 해를 찾는 데 사용되며, 선택(Selection), 교차(Crossover), 변이(Mutation) 등의 개념을 활용하여 문제를 해결합니다. 각 단계에서의 개념을 설명하고 어떻게 최적의 해를 찾는지 설명드리겠습니다. 아래는 Genetic Algorithm을 도식화 한 그림입니다.

초기 집단 생성 (Initialization)
유전 알고리즘은 여러 해(solution)를 한 번에 다루며, 이 해들은 염색체(Chromosomes) 또는 유전자(Genes)라고 불립니다. 처음에는 무작위로 여러 개의 해(개체) 집단을 생성하는데, 이를 **초기 집단(Population)**이라고 합니다. 각 개체는 문제의 잠재적인 해를 나타내며, 보통 이진수(0과 1) 또는 실수로 표현됩니다.
(만약 4개의 염색체가 존재한다고 했을 때 각 개체들은 아래와 같은 방식으로 표현이 될 수 있습니다.)
- 개체 1: 101011
- 개체 2: 110110
- 개체 3: 011001
- 개체 4: 100101
적합도 평가 (Fitness Evaluation)
각 염색체의 성능을 평가하기 위해 **적합도 함수(Fitness Function)**를 사용합니다. 이 함수는 염색체 문제의 최적 해에 얼마나 가까운지를 평가합니다. 적합도가 높은 개체는 더 나은 해를 나타내며, 다음 세대로 선택될 확률이 높아집니다.
선택 (Selection)
다음 세대를 만들기 위해 부모 개체를 선택하는 과정입니다. 적합도가 높은 개체들이 더 많이 선택될 가능성이 큽니다. 룰렛 휠 선택(Roulette Wheel Selection) 방법이 자주 사용됩니다.
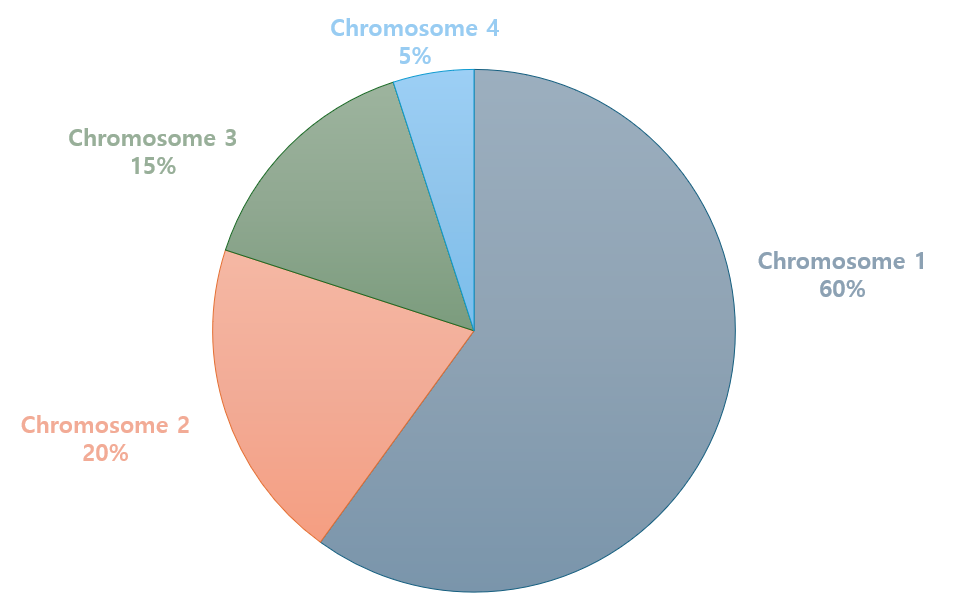
적합도 함수를 통해 각 염색체 마다 적합도가 나오게 되는데 적합도가 높은 개체일수록 선택될 확률이 큽니다. (즉, 적합도에 비례하게 염색체가 선택됨)
- 1번 염색체 선택확률 : 60%
- 2번 염색체 선택확률 : 20%
- 3번 염색체 선택확률 : 15%
- 4번 염색체 선택확률 : 5%
교차 (Crossover)
두 부모 개체로부터 자손을 생성하는 과정입니다. 교차는 부모 개체의 유전자를 섞어 새로운 자손을 만드는 방식으로 이루어집니다. 대표적인 방법으로는 단일 교차(single-point crossover), 다중 교차(multi-point crossover), 균등 교차(uniform crossover) 등이 있습니다. 저는 단일 교차에 대해서 설명드리도록 하겠습니다.


Simple crossover은 2개 부모 염색체를 합쳐서 자손을 생성합니다. 이때 Division point를 기준으로 왼쪽은 Parent1, 오른쪽은 Parent2의 정보를 가진 자손이 생성됩니다.
부모 1 : 1 0 1 0 0
부모 2 : 0 0 0 1 1
새로운 자손 : 1 0(부모 1 data) | 0 1 1(부모2 data)
변이 (Mutation)
변이는 자손의 유전자 일부를 무작위로 변경하는 과정입니다. 이를 통해 다양성을 유지하고 새로운 해를 탐색할 수 있습니다. 변이는 보통 매우 낮은 확률(5%)로 발생합니다. 예를 들어, 이진수로 표현된 유전자의 일부를 반대로 바꿔줍니다
생성된 자손 염색체에서 일정 확률(e.g. 0.01)에 포함되는 유전자에 [1인 경우 -> 0으로], [0인 경우 -> 1로] 바꿔주는 reverse 과정이 진행됩니다.
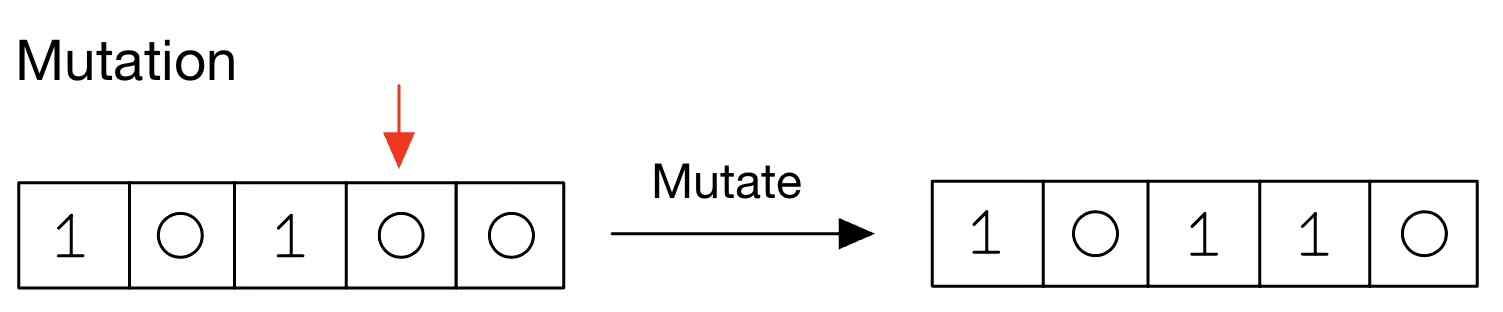
- 자손1: 10100 → 10110 (변이 발생)
Create Offspring
최종적으로 선택, 교차, 변이를 통하여 자손이 생성되게 됩니다.
종료 조건 (Termination Condition)
알고리즘은 일반적으로 다음과 같은 조건 중 하나를 만족할 때 종료됩니다.
- 최대 세대 수에 도달했을 때(위 그림에서는 iteration이 100번으로 설정되었습니다.)
- 여기서 세대(Generation)란, 유전 알고리즘에서는 한 세대는 선택, 교차, 변이의 과정이 한 번 끝날 때까지의 단계를 의미합니다. 각 세대에서 새로운 자손들이 생성되고, 그 자손들이 새로운 집단을 형성합니다.
- Iteration(반복)은 유전 알고리즘에서 한 번의 세대가 끝나고 다음 세대로 넘어가는 과정을 반복하게 됩니다. 이 반복되는 횟수를 iteration이라고 부릅니다.
- 적합도가 특정 값 이상으로 높아졌을 때
- 적합도 변화가 거의 없을 때 (수렴)
종료조건 후에 생성된 자손이 최종적으로 선택된 변수라고 볼 수 있습니다.
유전 알고리즘은 다양한 최적화 문제를 해결할 수 있지만, 최적해를 보장하지는 않으며, 해의 품질과 속도는 파라미터 설정(교차율, 변이율 등)에 크게 영향을 받습니다.
Example
아래는 baseball data를 통해 AIC가 가장 낮게 나오는 변수를 선택하는 유전알고리즘을 만들었습니다.
이때 iteration은 100번, 염색체의 길이는 27개(01001….10 이런 방식(총 길이가 27)), 27개의 길이를 가지는 20개의 랜덤한 개체를 생성하였고, mutate는 1%로 설정하여 최적해를 구했습니다. 이때 적합도 함수는 $\frac{2r_i}{P(P+1)}$로 설정했습니다.
주석을 달아놨으니 확인하실 수 있습니다.
# Import
import numpy as np
import pandas as pd
import statsmodels.api as sm
from scipy.stats import rankdata
# Load Data
data = pd.read_csv('/content/baseball.dat', sep=' ')
X = data.drop('salary', axis=1) # predictors
y = np.log(data['salary']) # response variable
# 초기값 설정
# 100(G)세대를 사용하고, 각 세대마다 개체의 수를 20(P)으로 설정
P = 20
G = 100
C = 27 # chromosomes of length C = 27
Mutation_rate = 0.01 # Apply 1% mutation
# 랜덤 시드 설정
np.random.seed(1)
# The starting generation consisted of purely random individuals.
Binary_generator = np.random.randint(2, size=(P, C))
# AIC 계산 함수(Minimize 하는 것이 목적)
def function_aic(X, y):
if np.sum(X)==0:
print("☆☆ 변수가 한개도 선택이 되지 않았기 때문에 다시 선택하시길 바랍니다. ☆☆")
return np.inf
model = sm.OLS(y, sm.add_constant(X)).fit()
return model.aic
# 적합도 계산 함수
def fitness(Binary_generator, data):
y = np.log(data['salary']).values
X = data.drop(columns=['salary']).values
# Binary_generator에서 1이라고 입력된 변수들을 독립변수로 사용하고 0으로 입력된 변수들은 제거하고 나서 AIC 측정
aics = np.array([function_aic(X[:, x == 1], y) for x in Binary_generator])
rank=rankdata(-aics) # 낮은 AIC가 높은 순위 이므로 -AIC에서 순위 측정
fitness_rank = 2 * rank / (P * (P + 1))
return fitness_rank
# 선택 연산자 : 적합도 함수에 기반하여 부모 염색체 생성
# Roulette Wheel Selection
def selection(fitness_scores):
numbers=np.arange(P)
probabilities=fitness_scores
choice=np.random.choice(numbers,p=probabilities/probabilities.sum())
return choice
# 두 부모의 염색체들로부터 하나의 자손염색체 생성하는 함수. Use Simple crossover!
def crossover(parent1, parent2):
point = np.random.randint(1, C) # Division point
child = np.concatenate([parent1[:point], parent2[point:]])
return child
# 돌연변이 적용 : 0.01보다 작은 index가 존재하면 [0 -> 1], [1 -> 0] 으로 reverse 수행
def mutate(child):
mutation_mask = np.random.rand(C) < Mutation_rate
child[mutation_mask] = 1 - child[mutation_mask]
return child
# 선택, 교차, 돌연변이 과정을 통해 새로운 자손 생성하는 함수
def create_generation(Binary_generator, fitness_scores):
new_Binary_generator = []
while len(new_Binary_generator) < P:
# 적합도 가중치 비율 이용해 부모 2개 select
parent1 = Binary_generator[selection(fitness_scores)]
parent2 = Binary_generator[selection(fitness_scores)]
# 부모를 섞어서 자손 생성
child = crossover(parent1, parent2)
# 자손 돌연변이
child = mutate(child)
new_Binary_generator.append(child)
return np.array(new_Binary_generator)
for generation in range(G):
# Rank-based fitness function을 사용해 적합도 계산
fitness_scores = fitness(Binary_generator, data)
# 선택, 교차, 돌연변이 연산자를 통해 새로운 자손 생성 -> 자손들이 다음에는 부모가 됨
Binary_generator = create_generation(Binary_generator, fitness_scores)
# 최종 결과
final_fitness = fitness(Binary_generator, data)
best_solution_index = np.argmax(final_fitness)
best_solution = Binary_generator[best_solution_index]
# 마지막 세대 각 개체의 적합도
print(f"마지막 세대의 각 개체 적합도는 다음과 같습니다. :{final_fitness}")
# 변수 이름 추출 하기 위함
column_names = X.columns
selected_variable_names = column_names[best_solution == 1]
# AIC가 가장 낮은 개체
print(f"선택된 변수는 다음과 같습니다. : {list(selected_variable_names)}")
# AIC가 가장 낮은 개체의 Index
print(f"선택된 개체의 인덱스는 다음과 같습니다. :{best_solution_index}")
감사합니다.
'머신러닝' 카테고리의 다른 글
| [머신러닝] SMOTE(Synthetic Minority Over-sampling Technique) (1) | 2024.09.13 |
|---|---|
| [머신러닝] Oversampling & Undersampling (0) | 2024.09.11 |
| [머신러닝] Graphical Models (2) | 2024.05.20 |