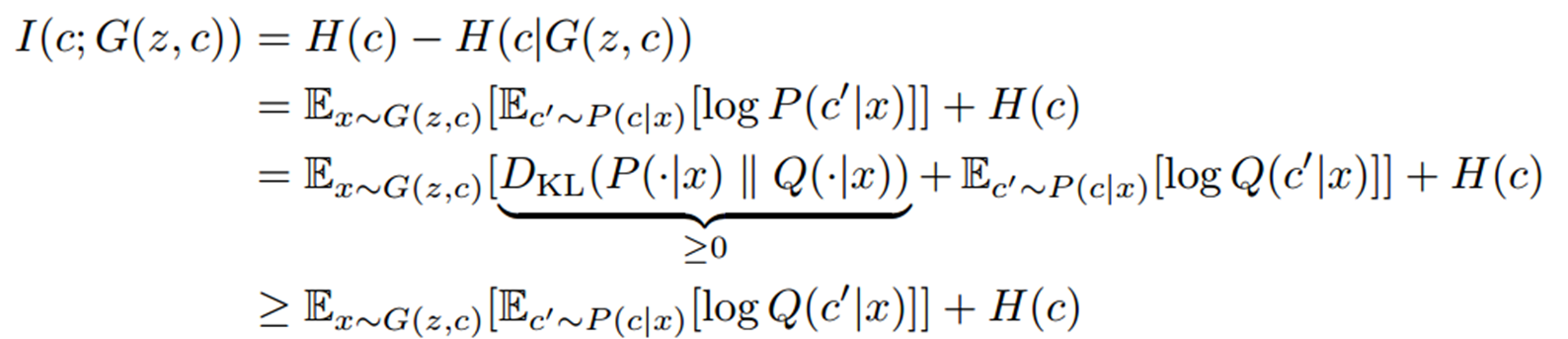이번 글에서는 2023년 AISTATS에서 발표된 Adversarial Random Forests for Density Estimation and Generative Modeling 논문에 대해 다뤄보도록 하겠습니다.
(랜덤포레스트 모델에 기반해서 데이터 생성할 수 있다는 것이 놀라웠고, 이 분야쪽은 아직 활발히 진행된 것 같지 않아서 깊게 파보면 좋은 모델을 만들어내는데 도움이 될 것 같은 느낌이 든다,,!)
Abstract
저자는 비지도 방식의 Random forest를 활용하여 데이터 생성하고, 밀도 추정에 대한 방법론을 제시하고자 합니다. GAN 모델에 영감을 받아서 생성자와 판별기가 반복적으로 학습하여 트리가 데이터의 구조적 특징을 학습하는 절차를 수행합니다.
이 방법은 최소한의 가정만으로 consistent를 보장한다고 강조하고 있으며, 저자의 방법론은 smooth한 밀도 추정을 제공하여 조금 더 자연스러운 데이터 생성이 가능하다고 합니다.
저자는 Tabular data를 생성하는 딥러닝 모델과 성능을 비교하고 있으며, 실행 속도가 평균적으로 훨씬 빠르다는 점을 강조하고 있습니다.
크게 알고리즘의 형태를 보자면
ARF → FORDE → FORGE 이 순서로 알고리즘이 진행됩니다.
ARF : 분류기 학습
FORDE : ARF에서 학습한 분류기를 통해 각 리프노드에서의 파라미터 추정
FORGE : 추정된 파라미터를 통해 데이터 생성
이제는 ARF 알고리즘에 대해 설명할 것입니다.(분류기 학습하는데 중점을 둔 알고리즘에 대해서!)
ADVERSARIAL RANDOM FORESTS
이제 저자가 제안한 방법론에 대해서 자세하게 다뤄보겠습니다.
ARF(Adversarial Random Forest)는 URF(Unsupervised Random Forest)의 재귀적 변형으로, 각 리프 노드에서 데이터가 서로 독립적인 상태(jointly independent)가 되도록 하는 것이 목표입니다. 아마도 변수별로 독립적인 패턴을 파악하여 간결하고 일반화된 모델을 만드는 데 도움이 될 것 같습니다.
(다음 글에서 ARF 알고리즘의 pseudo code를 직접 뜯어보면서 더 자세하게 다룰 것입니다. 아래는 알고리즘의 흐름)
초기 단계: 먼저 기존의 URF를 합성 데이터 $\tilde{X}^{(0)}$로 학습하여 분류기 $f^{(0)}$을 생성합니다. 만약 분류기의 정확도가 50%이상이라면(생성데이터와 원본데이터의 구분 확률) 리프노드의 coverage를 계산하게 됩니다. 이때 coverage는 원본데이터에 대해서 계산하게 됩니다.(coverage라는건 원본데이터가 각 리프노드에 들어간 비율을 말합니다.) 각 리프 노드의 커버리지를 계산한 후, 이 비율에 따라 리프 노드를 무작위로 선택하고, 그 안의 마진으로부터 새로운 합성 데이터셋 $\tilde{X}^{(1)}$을 생성합니다. (커버리지가 높을수록 그 리프에서의 데이터 생성 개수는 많아짐) 생성된 합성 데이터 $\tilde{X}^{(1)}$과 원본 데이터 $X$를 구분하는 새로운 분류기 $f^{(1)}$을 학습합니다.(ARF 알고리즘에서 분류기를 학습하고 나서 그 분류기를 통해 밀도추정(FORDE)과 데이터 생성(FORGE)하는 것임! ARF는 분류기 학습에 중점을 두는 것이지 데이터 생성하는것이 목적이 아닌것을 알아두자!)
새로운 분류기의 OOB(Out-of-Bag) 정확도가 충분히 낮아지면 ARF가 수렴한 것으로 간주하고, $f^{(1)}$를 최종 모델로 사용합니다. 그렇지 않다면, 위의 과정을 반복하여 새로운 합성 데이터셋을 생성하고 분류기를 학습합니다. → 수렴할때까지!
- 수렴의 의미
- 수렴한다는 것은 ARF의 분류기가 더 이상 합성 데이터와 원본 데이터를 구분할 수 없게 되었다는 것을 의미합니다. 즉, 합성 데이터가 원본 데이터와 매우 유사해져서 분류기의 정확도가 대략 50%에 도달한 상태를 말합니다. 이때를 수렴한다고 말하고 있습니다.
- OOB(Out-of-Bag) 정확도란?
- 랜덤 포레스트(Random Forest)에서 모델 성능을 평가할 때 사용하는 방법이며, 선택되지 않은 샘플을 활용하여 모델의 성능을 측정합니다. (부트스트랩 샘플링을 사용하면 데이터의 63%정도가 각 트리의 학습에 사용되고, 나머지 37%는 사용되지 않습니다. 각 트리에서 n개의 샘플을 복원추출로 뽑는다고 생각하면 한개의 샘플이 뽑히지 않을 확률은 (1-$\frac{1}{n}$)입니다. 트리가 무한대로 증가하면 $\lim\limits_{n\rightarrow \infin}(1-\frac{1}{n})^n$=$e^{-1}$ ≈ 0.3678794 )
- 각 트리에 대해 OOB 샘플을 사용해 정확도를 측정하고, 모든 트리의 결과를 평균하여 최종 OOB 정확도를 계산합니다. → 충분히 낮다면 ARF수렴
ARF(Adversarial Random Forest)는 GAN과 유사한 구조를 가지고 있지만 몇 가지 중요한 차이점이 있습니다.
- 유사점
- ARF에서의 "생성자"는 marginal distribution에서 샘플링하여 데이터를 생성하는 역할을 하고, "판별자"는 랜덤 포레스트 분류기입니다. 이 둘은 서로 번갈아 가며 레이블 불확실성을 높이고 낮추는 제로섬 게임 형태로 작동합니다.
- 차이점
- 파라미터 공유: ARF에서는 생성자와 판별자가 동일한 파라미터를 공유합니다. GAN에서는 생성자와 판별자가 뉴럴네트워크를 통해 파라미터를 학습했지만, ARF에서 생성자는 스스로 학습하지 않고 판별자가 학습한 정보를 활용하는 방식입니다.
- ARF모델에서 합성 데이터는 원본데이터들을 이용하여 복원추출한 데이터입니다. 즉, 새롭게 생성한 데이터가 아닌 것입니다! → ARF 알고리즘에서는 데이터를 독립적으로 만드는 leaf를 학습하는데 중점을 두고있습니다. 새로운 데이터를 생성하는 것은 FORDE를 통해 분포에 대한 parameter를 학습하고 FORGE에서 새로운 데이터를 생성합니다!
- ARF는 한 번의 반복만으로도 데이터의 독립성을 유도할 수도 있다고 합니다.
위에서는 ARF 모델에 대한 흐름을 설명하였고 이제는 각 리프노드에서 변수들 간의 독립성을 만족시키기 위한 조건에 대해 살펴보겠습니다! (가장 중요한 부분! 변수간 독립이 만족하지 못하면 의미가 없음)
ARF(Adversarial Random Forest)가 데이터의 독립성을 확보하고 수렴하는 데 필요한 조건과 가정에 대해 설명하겠습니다.
Local Independence Criterion
- 목표: ARF의 목표는 각 트리의 모든 리프 노드에서 데이터가 독립적으로 분포하도록 분할을 수행하는 것입니다. 모든 트리 b, 리프 노드 $\ell$, 그리고 샘플 x에 대해 다음을 만족하는 분할 세트 Θ를 찾는 것입니다. $p(x|\theta^\ell_b)=\prod^d_{j=1}p(x_j|\theta^\ell_b)$. 즉, 각 리프 노드에서 데이터의 joint probability가 각 변수들의 곱으로 표현될 수 있음을 의미하며 각 노드 내에서 변수들이 독립이라는 것을 말할 수 있습니다.
Assumption 1 : 특성 도메인 가정
- 특성 공간 제한: 특성 공간이 $X=[0,1]^d$로 제한되어 있으며, 이 범위 내에서 joint density p가 0과 ∞ 사이에서 안정적으로 유지된다는 가정입니다. 이는 데이터가 모든 특성에 대해 정상적인 분포를 가지고 있고, 특성 값들이 정해진 범위 내에서 벗어나지 않음을 의미합니다.
Assumption 2 : Lipschitz 연속성 가정
- Lipschitz 연속성: 각 라운드마다 목표 함수 P(Y=1∣x)가 Lipschitz 연속성을 만족해야 한다는 가정입니다.
- Lipschitz 연속성은 함수의 변화 속도가 특정한 상수(즉, Lipschitz 상수)로 제한된다는 것을 의미합니다. Lipschitz 상수가 매 라운드마다 바뀔 수 있지만, 이 값이 $\frac{1}{max_{\ell,b}(diam(X^\ell_b))}$
- 이 가정은 데이터 분포가 과도하게 변화하지 않도록 하여 안정적인 학습을 보장합니다.
Assumption 3 : 트리 구성 및 학습에 관한 조건
이 가정은 ARF에서 사용되는 트리 구조에 대한 여러 가지 조건을 설정합니다.
- (i) 트레이닝 데이터 분할: 각 트리를 학습할 때, 데이터를 두 부분으로 나눕니다:
- 하나는 분할 기준을 학습하기 위한 부분이고,
- 다른 하나는 리프 노드에 레이블을 할당하기 위한 부분입니다.
- (ii) 트리의 성장 방식:
- 각 트리는 부트스트랩 샘플링이 아닌 subsamples(중복 허용x)를 사용해 학습됩니다.
- 부트스트랩 샘플링으로 학습되면 과적합이 발생할 수도 있기 때문!
- 이라고 하는데, 실제 코드 뜯어보니 부트스트랩 샘플링으로 트리를 학습하는 것 같은데,,, 혹시나 보신 분이 있다면 의견 부탁드립니다. (_ _)
- 트리 학습할 때 subsampling하려면 ranger함수에서 수정을 해야할 듯 함(뇌피셜)
- subsamples의 크기 $n_b$(트리b에서 학습에 사용되는 데이터 수)는 n보다 작아야 합니다. ($n_b$→∞, $n_b$/**$n$**→0 as **$n$**→ ∞).
- 각 트리는 부트스트랩 샘플링이 아닌 subsamples(중복 허용x)를 사용해 학습됩니다.
- (iii) 분할 확률:
- 각 내부 노드에서 특정 특성 $X_j$를 분할할 확률은 최소 π>0으로 제한됩니다.
- 예를 들어 키와 몸무게에 대한 변수가 있다면, 처음 루트노드에서 키를 선택할지 몸무게를 선택할지에 대한 확률을 부여해줘야 합니다. 즉, 특정 특성에만 의존하지 않도록 합니다.
- 각 내부 노드에서 특정 특성 $X_j$를 분할할 확률은 최소 π>0으로 제한됩니다.
- (iv) 분할의 균형성:
- 각 분할에서 두 자식 노드에 들어가는 데이터 비율은 최소한 γ∈(0,0.5]이어야 합니다.
- 이 부분은 자식노드에 최소한의 비율을 보장하기 위해서 설정한 것입니다. 만약 설정하지 않게되면 두개의 자식노드의 비율이 0.99, 0.01 이렇게 분할이 되는 상황이 발생할 수도 있기 때문입니다.
- 각 분할에서 두 자식 노드에 들어가는 데이터 비율은 최소한 γ∈(0,0.5]이어야 합니다.
- (v) 리프 노드의 개수:
- 각 트리 b에 대해 리프 노드의 총 개수 $L_b$는 ∞로 향해야 하지만, 전체 데이터 수 n에 비해 작아야 합니다. ($L_b$→∞, $L_b$/**$n$**→0 as **$n$**→ ∞).
- (vi) 소프트 레이블:
- 각 노드의 예측 확률을 투표가 아닌 평균을 통해 결정한다는 의미입니다.
ARF는 특성 독립성을 확보하고 데이터를 효과적으로 분할하기 위해 위의 가정들(A1~A3)을 만족하는 환경에서 작동합니다. 이러한 가정들은 ARF가 수렴하고, 리프 노드에서 데이터의 독립성을 확보하여 밀도 추정 및 데이터 생성에 적합한 모델을 학습하는 데 필수적인 역할을 합니다.
- 데이터의 변수들이 독립이 되는것을 아주 강조하는걸 보니 독립이냐 아니냐에 따라 모델의 성능을 좌지우지하는 것 같다는 생각이 드네요(어쩌면 독립이 아니라면 성능이 너무 낮게 나올수도)
Density Estimation and Data Synthesis
ARF에서 변수별 독립을 만족시키기 위한 가정들을 살펴보았고, ARF알고리즘을 통해 분류기를 생성하고 그 분류기를 활용하여 Density 추정과 데이터 생성하는 파트에 대해 설명하겠습니다.
ARF(Adversarial Random Forest)는 두 가지 알고리즘인 FORDE(FORests for Density Estimation)와 FORGE(FORests for GEnerative modeling)의 기반이 됩니다. [위에서 말했듯이 ARF알고리즘을 통해 분류기 생성 → 그 분류기를 이용해 density 추정(FORDE) → density를 통해 각 변수별 데이터 생성(FORGE)]
이 두 알고리즘에서 local independence criterion을 활용해 각 리프 노드 내에서 다변량 밀도 추정 대신 d개의 개별 단변량 밀도 추정기를 실행합니다. 이는 고차원 데이터에서 발생하는 차원의 저주를 피할 수 있기 때문에 훨씬 효율적입니다. 실제로 고차원 데이터에서 전통적인 커널 밀도 추정(KDE)은 차원의 제약으로 인해 잘 작동하지 않지만, ARF는 독립성을 확보하는 분할을 학습함으로써 밀도 추정과 데이터 생성에 더 효과적이고 효율적으로 대응할 수 있습니다.
- 여기서 차원의 저주를 피할 수 있다고 말하는 이유는, ARF가 각 변수들 간의 독립성을 확보함으로써 각 변수에 대해 개별적으로 밀도 추정을 할 수 있기 때문입니다. 일반적으로 다변량 밀도 추정은 고차원 데이터에서 모든 특성 간의 결합 분포를 학습해야 하기 때문에, 차원의 저주(curse of dimensionality)라는 문제에 직면하게 됩니다. 이는 데이터의 차원이 높아질수록 추정해야 할 분포의 복잡성이 기하급수적으로 증가하기 때문입니다. 반면에, ARF의 경우 local independence criterion(각 변수들 간 독립!)에 따라 리프 노드 내에서 각 특성들이 독립적으로 분포하므로, 각 변수에 대해 단변량 밀도 추정(univariate density estimation)을 수행할 수 있습니다. 이를 통해 다변량 밀도 추정에서 발생하는 차원의 저주 문제를 효과적으로 피할 수 있게 됩니다.
ARF를 기반으로 FORDE와 FORGE 알고리즘이 다음과 같이 진행됩니다.
FORDE
- 각 트리 b에 대해 분할 기준 $\theta^\ell_b$와 각 리프 노드 $\ell$의 경험적 커버리지 $q(\theta^\ell_b)$를 기록합니다. 이것들을 리프 노드의 파라미터라고 부릅니다.
- 그런 다음 각 리프 노드에 대해, 원래 데이터의 각 특성 $X_j$에 대해 독립적으로 분포 파라미터 $\psi^\ell_{b,j}$를 추정합니다.
- 예를 들어, 연속형 데이터의 경우 커널 밀도 추정(KDE)의 대역폭이나 MLE를 활용해 추정합니다.
각 변수에 대한 파라미터 $\psi^\ell_{b,j}$학습
- 연속형 데이터의 경우 MLE를 사용하여 truncated Gaussian mixture model을 구현하고, 범주형 변수에 대해서는 베이지안 추론을 사용합니다. 이는 리프 노드에서 관찰되지 않은 값에 대해 극단적인 확률을 피하면서 리프 노드의 지원(support) 내에 있는 값을 반영하기 위함입니다.
FORGE
- 트리 선택: 전체 트리 집합 B에서 트리 b를 균등하게 무작위로 선택하고, 해당 트리에서 리프 노드 $\ell$)를 커버리지 확률 $q(\theta^\ell_b)$ 에 따라 선택합니다. 이는 ARF 알고리즘의 재귀적 반복에서 합성 데이터를 생성하는 방식과 동일합니다.
- 특성 샘플링: 각 특성 $X_j$에 대해, $\psi^\ell_{b,j}$에 의해 매개변수화된 밀도 또는 질량 함수에 따라 데이터를 샘플링합니다.
이렇게 데이터 생성을 했으니까 데이터 생성을 잘 했는지 확인할 필요가 있죠! 그러기 위해서 추정된 밀도와 실제 밀도를 비교합니다!
- 추정된 밀도 함수 $q(x)$는 다음과 같이 표현됩니다 $q(x)=\frac{1}{B}\sum\limits_{\ell,b:x\in X^\ell_b}q(\theta^\ell_b)\prod\limits_{j=1}^dq(x_j;\psi^\ell_{b,j}).$
- 여기서 B는 전체 트리의 수를 나타내고, 분포는 해당 리프 노드에 대한 커버리지 $q(\theta^\ell_b)$에 가중치가 부여된 모든 리프 노드의 평균값으로 나타납니다.
- 이때 $q(x_j;\psi^\ell_{b,j})$는 각 특성 $x_j$에 대한 밀도 함수입니다.($\psi^\ell_{b,j}$를 distribution의 parameter로 설정)
- **실제 밀도 함수 $p(x)$**는 다음과 같습니다
- 이 경우 역시 커버리지 확률$p(\theta^\ell_b)$로 가중치가 부여된 각 리프 노드의 밀도로 구성되어 있습니다.
- $p(x)=\frac{1}{B}\sum\limits_{\ell,b:x\in X^\ell_b}p(\theta^\ell_b)p(x|\theta^\ell_b).$
밀도 함수의 의미
- 추정된 밀도 $q(x)$와 실제 밀도 $p(x)$ 모두, 각 리프 노드에서의 분포를 가중치로 합산한 것으로 표현될 수 있습니다.
이 부분에서는 ARF(Adversarial Random Forest) 알고리즘의 손실 함수, 추가 가정, 그리고 발생할 수 있는 세 가지 오류에 대해 설명하고 있습니다.
손실 함수 (Loss Function)
- L2-consistency에 관심이 있기 때문에, 손실 함수는 평균 통합 제곱 오차(MISE, Mean Integrated Squared Error)로 정의됩니다. $MISE(p,q):=\mathbb{E}[\int_X(p(x)-q(x))^2dx].$
- 이는 밀도 추정의 정확성을 측정하는 지표로, $p(x)$와 $q(x)$가 얼마나 가까운지를 평가합니다.
추가 가정
- A4 : 실제 밀도 함수 p는 매끄럽다는 가정을 추가로 요구합니다.
- 두 번째 도함수 $p^{''}$가 유한하고, 연속적이며, square integrable하고, monotone해야 합니다.
- 이 가정은 커널 밀도 추정(KDE, Kernel Density Estimation)의 일관성을 보장하기 위한 표준 조건으로, ARF 분석에서 중요한 역할을 합니다.
ARF 방법론은 세 가지 잠재적인 오류를 가질 수 있습니다.
- Error of Coverage
- 정의: 리프 노드 ‘와 트리 b에 대해, 실제 커버리지 $p(\theta^\ell_b)$와 추정된 커버리지 $q(\theta^\ell_b)$의 차이입니다.
- 의미: 리프 노드의 커버리지가 실제 데이터와 얼마나 일치하는지를 나타내는 오류입니다.
- $\epsilon_1:=\epsilon_1(\ell,b):=p(\theta^\ell_b)-q(\theta^\ell_b)$
- Error of Density $\epsilon_2:=\epsilon_2(\ell,b,x):=\prod\limits_{j=1}^d p(x_j|\theta^\ell_b)-\prod\limits_{j=1}^dq(x_j;\psi^\ell_{b,j})$
- 정의: 리프 노드 $\ell$, 트리 b, 샘플 x에 대해, 실제 조건부 밀도 $\prod\limits_{j=1}^d p(x_j|\theta^\ell_b)$와 추정된 조건부 밀도 $\prod\limits_{j=1}^dq(x_j;\psi^\ell_{b,j})$의 차이입니다.
- 의미: 각 리프 노드 내에서 특성별로 독립적으로 추정된 밀도가 실제 밀도와 얼마나 다른지를 나타내는 오류입니다.
- Error of Convergence $\epsilon_3:=\epsilon_3(\ell,b,x):=p(x|\theta^\ell_b)-\prod\limits_{j=1}^d p(x_j|\theta^\ell_b)$
- 정의: 리프 노드 $\ell$, 트리 b, 샘플 x에 대해, 실제 조건부 밀도 $p(x|\theta^\ell_b)$와 특성별 조건부 밀도의 곱 $\prod\limits_{j=1}^d p(x_j|\theta^\ell_b)$의 차이입니다.
- 의미: 실제 조건부 밀도가 각 특성의 독립적 밀도의 곱과 얼마나 다른지를 나타내는 오류입니다. 이는 실제 데이터가 특성 간에 종속성을 가질 경우 발생할 수 있습니다.
- $\epsilon_1$ : 리프 노드 $\ell$와 트리 b에 따라 달라지는 랜덤 변수입니다.
- $\epsilon_{2,3}$ 리프 노드 $\ell$, 트리 b, 그리고 샘플 x에 따라 달라지는 랜덤 변수입니다.
이러한 가정들과 오류 정의를 통해 ARF는 consistency을 보장하고, 효과적인 데이터 생성 및 분포 학습을 수행할 수 있습니다.
Experiments

- 위 그림은 ARF 모델을 사용하여 데이터 생성하였습니다. ARF모델이 생각보다 데이터 생성을 잘 하고 있는 것을 볼 수 있습니다.

- 또한 ARF를 이용해 데이터 생성한 모델과 다른 딥러닝 모델의 성능을 비교해 보았습니다. 어떤 경우에는 FORGE가 성능이 높고 다른 데이터셋에선 다른 딥러닝의 모델이 성능이 높지만, ARF의 모델이 성능이 뒤쳐지지 않을뿐 아니라 가장 빠르게 학습을 할 수 있다는 것입니다. 시간측면에서는 월등히 앞서는 것을 볼 수 있습니다.
다음 글에서 ARF, FORDE, FORGE 알고리즘의 pseudo code를 깃허브에 제공되어있는 R코드와 함께 살펴보면서 각 단계별로 모델이 어떤 흐름으로 진행되는지 확인해보도록 하겠습니다.
감사합니다.
'논문 리뷰 > Generative model' 카테고리의 다른 글
| [CTGAN] Modeling Tabular Data using Conditional GAN (0) | 2024.05.14 |
|---|---|
| [InfoGAN] Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets (1) | 2024.04.08 |